원에 대하여

가상의 한 점에서 같은 거리 만큼 떨어진 점들의 집합을 원이라 할수 있다. 한 점(원점)에서 1의 거리 만큼 떨어진 점들의 모임인 단위원을 생각해 보자. \( x^2 + y^2 = 1^2 \)인 원의 공식을 기억할지 모르겠다.

이론적 배경

가상의 한 점에서 같은 거리 만큼 떨어진 점들의 집합을 원이라 할수 있다. 한 점(원점)에서 1의 거리 만큼 떨어진 점들의 모임인 단위원을 생각해 보자. \( x^2 + y^2 = 1^2 \)인 원의 공식을 기억할지 모르겠다. 중학교 수학 시간에 배운 기억이 어렴풋이 나지 않는가?

그러면 한 점에서 1만큼 떨어진 위치에 꼭지점을 갖는 정n각형을 생각하자. 정삼각형, 정사각형, 정오각형 무수히 많다. 그러면 n의 수가 커질수록 이 정다각형의 모양은 원에 가깝게 된다.

이러한 사실을 다음 과정을 수행하는 R 시각화를 이용해서 증명해 보자.

1. \( x^2 + y^2 = 1^2 \)인 단위원을 그린다. 이 원은 n각형의 외접원이 될 것이다.
2. \( x^2 + y^2 = cos( {n })^2 \)인 단위원을 그린다. 이 원은 n각형의 내접원이 될 것이다.
3. 원점에서 1만큼 떨어진 곳에 n개의 점을 찍고 이 점을 연결한 n각형을 그린다.

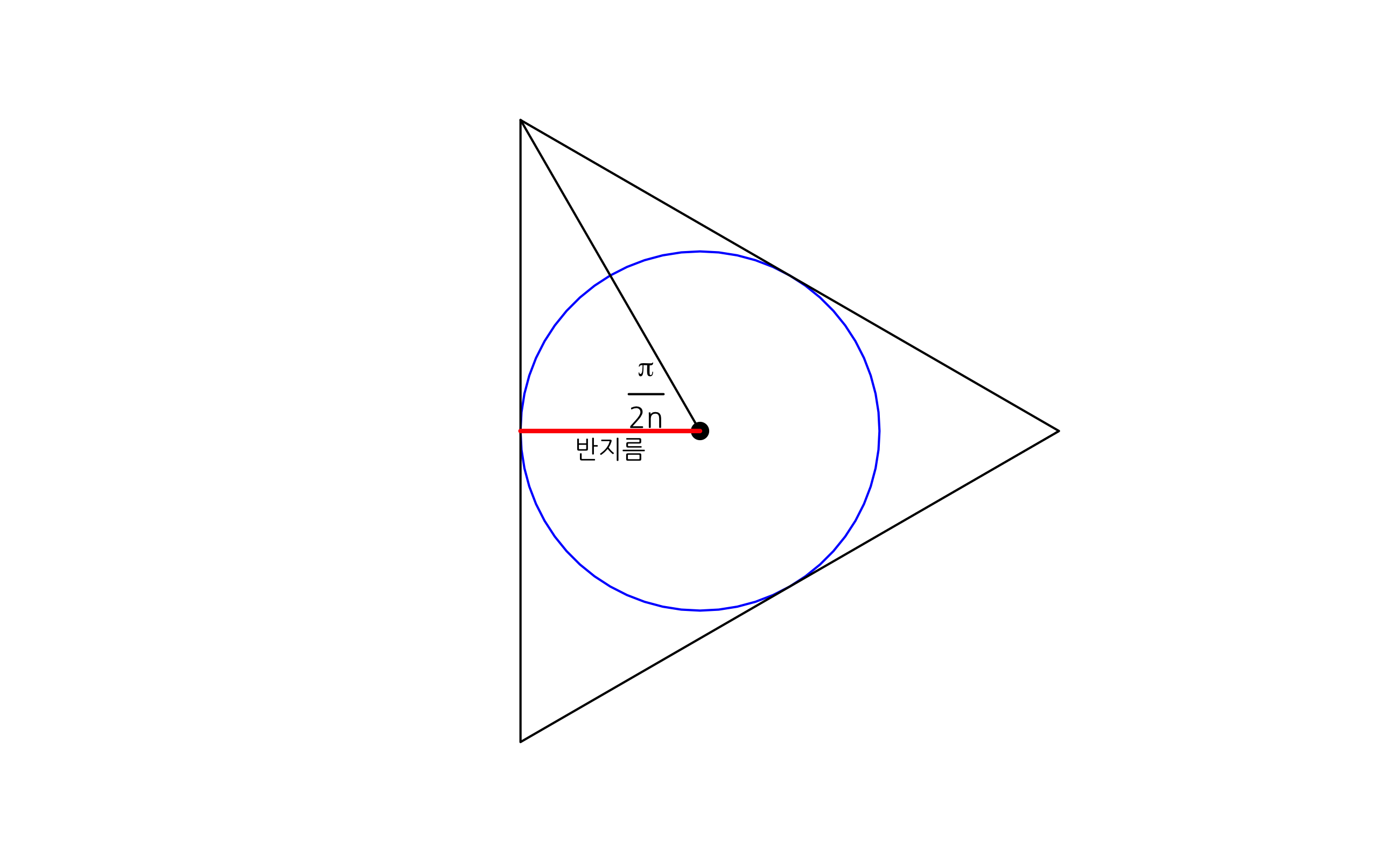
내접원의 반지름이 \( cos( {n}) \)인 이유는 다음과 같다.

n각형의 중심에서 각각의 꼭지점을 잇는 선을 그리면 n개의 동일한 면적의 이등변 삼각형이 만들어 진다. 그리고 이 이등변삼각형을 반으로 나누면 두개의 직각 삼각형이 되는데 이 직각삼각형의 원점에서의 각이 \( \)인 직각삼각형이고, 내접원의 반지름은 \( r cos() \)이므로 \( cos() \)이 된다.

R 시각화

내접원과 외접원을 그리는 R 코드와 결과는 다음과 같다.

par(family='NanumGothic')

radius <- function () {
  par(mfrow = c(1, 1), mar=c(1, 1, 1, 1), pty = 's')
  
  plot(c(-1, 1), c(-1, 1), type = 'n', 
       axes = FALSE, xlab = '', ylab = '')
 
  angle <- (0:(10 * 6)) / (10 * 6) * 2 * pi
  x1 <- cos(angle) / 2
  y1 <- sin(angle) / 2
  
  lines(x1, y1, col = "blue")
  x <- rep(0, 3)
  y <- rep(0, 3)
  
  for (i in 0:3) {
   x[i+1] <- cos(angle[i * 20 + 1])
   y[i+1] <- sin(angle[i * 20 + 1])
   }
  
  lines(x, y)
  points(0,0, pch = 19)
  lines(c(0, x[2]), c(0, y[2]))
  lines(c(0, cos(pi) / 2), c(0, 0), col = "red", lwd = 2)
  
  text(cos(pi) / 4, -0.05, "반지름", cex = 0.7)
  text(-0.15, 0.1, labels = expression(frac(pi, 2 * n)), 
       cex = 0.8)
}

radius()

원으로의 수렴

그러면 앞의 방법으로 \(n\)각형과 내접원, 외접원을 그려보자. \(n\)이 클수록 다각형은 원에 가까워지고, 내접원과 외접원의 크기도 점점 같아지게 된다. 즉, 원에 가까워진다는 반증이다.

정 3, 6, 9, 12각형을 그려보자.

circle <- function (points) {
  par(pty = 's')
  
  plot(c(-1, 1), c(-1, 1), type = 'n', 
       axes = FALSE, xlab = '', ylab = '')
  
  angle <- (0:(10 * points)) / (10 * points) * 2 * pi
  x1 <- cos(2 * pi / (points * 2)) * cos(angle)
  y1 <- cos(2 * pi / (points * 2)) * sin(angle)
  x2 <- cos(angle)
  y2 <- sin(angle)
  
  lines(x1, y1, col = "blue")
  lines(x2, y2)
  
  x <- rep(0, points)
  y <- rep(0, points)
  
  for (i in 0:points) {
    x[i+1] <- cos(angle[i * 10 + 1])
    y[i+1] <- sin(angle[i * 10 + 1])
  }
 
  lines(x, y, col = "red", lwd = 1.7)
}

par(mfrow = c(2, 2), mar = c(1, 1, 1, 1))
circle(3)
circle(6)
circle(12)
circle(30)

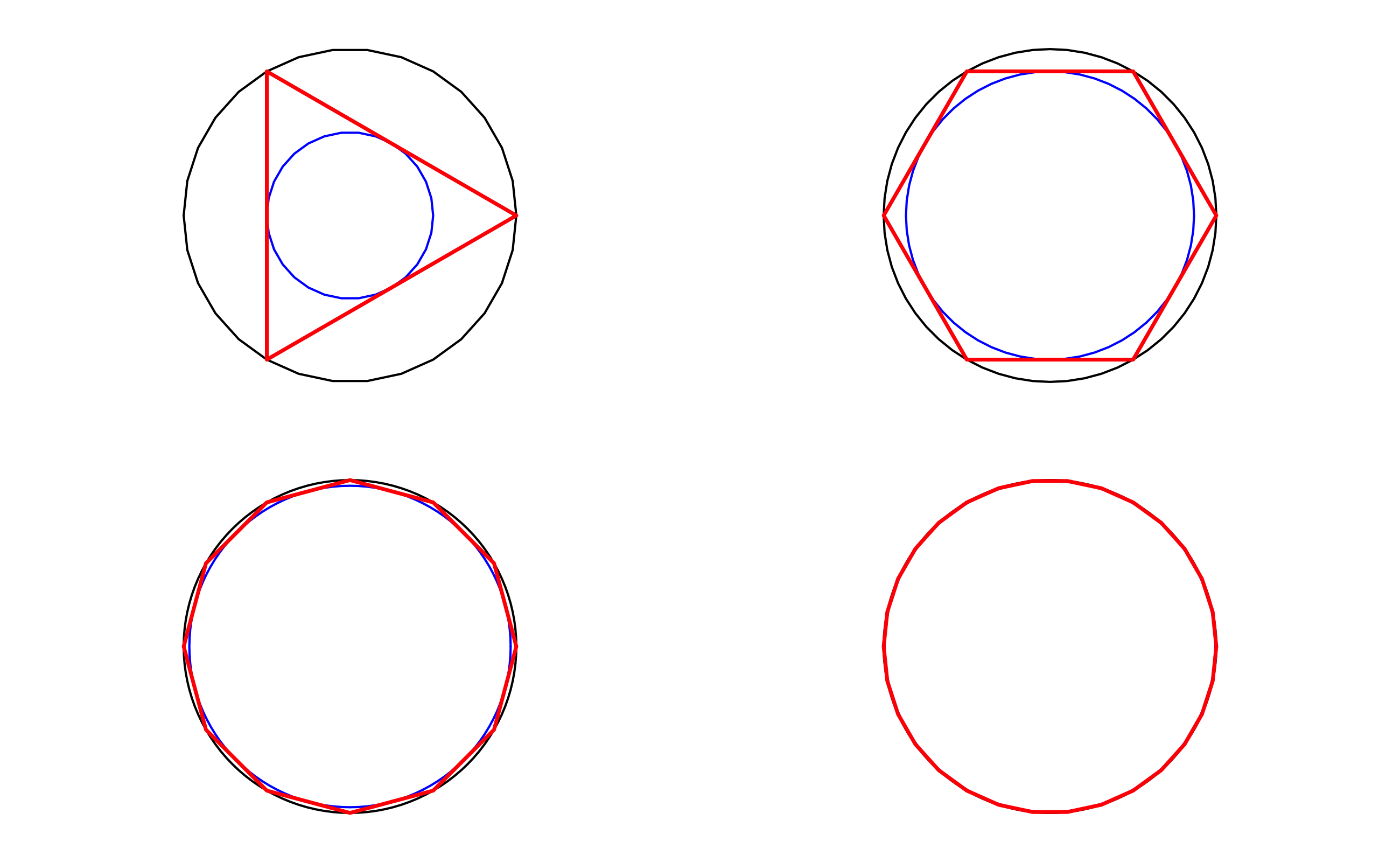
circle() 함수로 정30각형만 그려도 거의 원과 구분되지 않는다. 물론 반지름이 1인 경우이다. 여기서 1이라 함은 graphics device에서의 절대좌표 크기다. 실생활에서 그림을 그릴 때, 반지름이 1미터라고 한다면 30각형은 원으로 보기 어려울 것이다. 단지 R의 graphics device 세계에서 원의 성질을 보여주는 예로 이해하기 바란다.