Preface
After you have acquired the data, you should do the following:
- Diagnose data quality.
- If there is a problem with data quality,
- The data must be corrected or re-acquired.
- Explore data to understand the data and find scenarios for performing the analysis.
- Derive new variables or perform variable transformations.
The dlookr package makes these steps fast and easy:
- Performs a data diagnosis or automatically generates a data diagnosis report.
- Discover data in various ways, and automatically generate EDA(exploratory data analysis) report.
- Impute missing values and outliers, resolve skewed data, and categorize continuous variables into categorical variables. And generates an automated report to support it.
This document introduces EDA(Exploratory Data
Analysis) methods provided by the dlookr package. You will
learn how to EDA of tbl_df data that inherits from
data.frame and data.frame with functions provided by
dlookr.
dlookr increases synergy with dplyr. Particularly in
data exploration and data wrangling, it increases the efficiency of the
tidyverse package group.
Supported data structures
Data diagnosis supports the following data structures.
- data frame: data.frame class.
- data table: tbl_df class.
-
table of DBMS: table of the DBMS through tbl_dbi.
- Use dplyr as the back-end interface for any DBI-compatible database.
datasets
To illustrate the primary use of EDA in the dlookr package, I use a
Carseats dataset. Carseats in the
ISLR package is a simulated data set containing sales of
child car seats at 400 stores. This data is a data.frame created to
predict sales volume.
str(Carseats)
'data.frame': 400 obs. of 11 variables:
$ Sales : num 9.5 11.22 10.06 7.4 4.15 ...
$ CompPrice : num 138 111 113 117 141 124 115 136 132 132 ...
$ Income : num 73 48 35 100 64 113 105 81 110 113 ...
$ Advertising: num 11 16 10 4 3 13 0 15 0 0 ...
$ Population : num 276 260 269 466 340 501 45 425 108 131 ...
$ Price : num 120 83 80 97 128 72 108 120 124 124 ...
$ ShelveLoc : Factor w/ 3 levels "Bad","Good","Medium": 1 2 3 3 1 1 3 2 3 3 ...
$ Age : num 42 65 59 55 38 78 71 67 76 76 ...
$ Education : num 17 10 12 14 13 16 15 10 10 17 ...
$ Urban : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 2 2 1 1 ...
$ US : Factor w/ 2 levels "No","Yes": 2 2 2 2 1 2 1 2 1 2 ...The contents of individual variables are as follows. (Refer to ISLR::Carseats Man page)
- Sales
- Unit sales (in thousands) at each location
- CompPrice
- Price charged by a competitor at each location
- Income
- Community income level (in thousands of dollars)
- Advertising
- Local advertising budget for company at each location (in thousands of dollars)
- Population
- Population size in region (in thousands)
- Price
- Price company charges for car seats at each site
- ShelveLoc
- A factor with levels of Bad, Good, and Medium indicating the quality of the shelving location for the car seats at each site
- Age
- Average age of the local population
- Education
- Education level at each location
- Urban
- A factor with levels No and Yes to indicate whether the store is in an urban or rural location
- US
- A factor with levels No and Yes to indicate whether the store is in the US or not
When data analysis is performed, data containing missing values is
frequently encountered. However, ‘Carseats’ is complete data without
missing values. So the following script created the missing values and
saved them as carseats.
carseats <- Carseats
suppressWarnings(RNGversion("3.5.0"))
set.seed(123)
carseats[sample(seq(NROW(carseats)), 20), "Income"] <- NA
suppressWarnings(RNGversion("3.5.0"))
set.seed(456)
carseats[sample(seq(NROW(carseats)), 10), "Urban"] <- NAExploratory Data Analysis
dlookr can help understand the distribution of data by calculating descriptive statistics of numerical data. In addition, the correlation between variables is identified, and a normality test is performed. It also identifies the relationship between target variables and independent variables.:
The following is a list of the EDA functions included in the dlookr package.:
-
describe()provides descriptive statistics for numerical data. -
normality()andplot_normality()perform normalization and visualization of numerical data. -
correlate()andplot.correlate()calculate the correlation coefficient between two numerical data and provide visualization. -
target_by()defines the target variable, andrelate()describes the relationship with the variables of interest corresponding to the target variable. -
plot.relate()visualizes the relationship to the variable of interest corresponding to the destination variable. -
eda_report()performs an exploratory data analysis and reports the results.
Univariate data EDA
Calculating descriptive statistics using
describe()
describe() computes descriptive statistics for numerical
data. Descriptive statistics help determine the distribution of
numerical variables. Like the function of dplyr, the first argument is
the tibble (or data frame). The second and subsequent arguments refer to
variables within that data frame.
The variables of the tbl_df object returned by
describe() are as follows.
-
n: number of observations excluding missing values -
na: number of missing values -
mean: arithmetic average -
sd: standard deviation -
se_mean: standard error mean. sd/sqrt(n) -
IQR: interquartile range (Q3-Q1) -
skewness: skewness -
kurtosis: kurtosis -
p25: Q1. 25% percentile -
p50: median. 50% percentile -
p75: Q3. 75% percentile -
p01,p05,p10,p20,p30: 1%, 5%, 20%, 30% percentiles -
p40,p60,p70,p80: 40%, 60%, 70%, 80% percentiles -
p90,p95,p99,p100: 90%, 95%, 99%, 100% percentiles
For example, describe() can compute the statistics of
all numerical variables in carseats:
describe(carseats)
[38;5;246m# A tibble: 8 × 26
[39m
described_variables n na mean sd se_mean IQR skewness kurtosis
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Sales 400 0 7.50 2.82 0.141 3.93 0.186 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m80
[4m9
[24m
[39m
[38;5;250m2
[39m CompPrice 400 0 125. 15.3 0.767 20 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m42
[4m8
[24m
[39m 0.041
[4m7
[24m
[38;5;250m3
[39m Income 380 20 68.9 28.1 1.44 48.2 0.044
[4m9
[24m -
[31m1
[39m
[31m.
[39m
[31m0
[39m
[31m9
[39m
[38;5;250m4
[39m Advertising 400 0 6.64 6.65 0.333 12 0.640 -
[31m0
[39m
[31m.
[39m
[31m545
[39m
[38;5;246m# ℹ 4 more rows
[39m
[38;5;246m# ℹ 17 more variables: p00 <dbl>, p01 <dbl>, p05 <dbl>, p10 <dbl>, p20 <dbl>,
[39m
[38;5;246m# p25 <dbl>, p30 <dbl>, p40 <dbl>, p50 <dbl>, p60 <dbl>, p70 <dbl>,
[39m
[38;5;246m# p75 <dbl>, p80 <dbl>, p90 <dbl>, p95 <dbl>, p99 <dbl>, p100 <dbl>
[39m-
skewness: The left-skewed distribution data, that is, the variables with significant positive skewness, should consider the log or sqrt transformations to follow the normal distribution. The variableAdvertisingseems to need to consider variable transformation. -
meanandsd,se_mean: ThePopulationwith a significantstandard error of the mean(se_mean) has low representativeness of thearithmetic mean(mean). Thestandard deviation(sd) is much more significant than the arithmetic average.
The following explains the descriptive statistics only for a few selected variables.:
# Select columns by name
describe(carseats, Sales, CompPrice, Income)
[38;5;246m# A tibble: 3 × 26
[39m
described_variables n na mean sd se_mean IQR skewness kurtosis
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Sales 400 0 7.50 2.82 0.141 3.93 0.186 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m80
[4m9
[24m
[39m
[38;5;250m2
[39m CompPrice 400 0 125. 15.3 0.767 20 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m42
[4m8
[24m
[39m 0.041
[4m7
[24m
[38;5;250m3
[39m Income 380 20 68.9 28.1 1.44 48.2 0.044
[4m9
[24m -
[31m1
[39m
[31m.
[39m
[31m0
[39m
[31m9
[39m
[38;5;246m# ℹ 17 more variables: p00 <dbl>, p01 <dbl>, p05 <dbl>, p10 <dbl>, p20 <dbl>,
[39m
[38;5;246m# p25 <dbl>, p30 <dbl>, p40 <dbl>, p50 <dbl>, p60 <dbl>, p70 <dbl>,
[39m
[38;5;246m# p75 <dbl>, p80 <dbl>, p90 <dbl>, p95 <dbl>, p99 <dbl>, p100 <dbl>
[39m
# Select all columns between year and day (include)
describe(carseats, Sales:Income)
[38;5;246m# A tibble: 3 × 26
[39m
described_variables n na mean sd se_mean IQR skewness kurtosis
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Sales 400 0 7.50 2.82 0.141 3.93 0.186 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m80
[4m9
[24m
[39m
[38;5;250m2
[39m CompPrice 400 0 125. 15.3 0.767 20 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m42
[4m8
[24m
[39m 0.041
[4m7
[24m
[38;5;250m3
[39m Income 380 20 68.9 28.1 1.44 48.2 0.044
[4m9
[24m -
[31m1
[39m
[31m.
[39m
[31m0
[39m
[31m9
[39m
[38;5;246m# ℹ 17 more variables: p00 <dbl>, p01 <dbl>, p05 <dbl>, p10 <dbl>, p20 <dbl>,
[39m
[38;5;246m# p25 <dbl>, p30 <dbl>, p40 <dbl>, p50 <dbl>, p60 <dbl>, p70 <dbl>,
[39m
[38;5;246m# p75 <dbl>, p80 <dbl>, p90 <dbl>, p95 <dbl>, p99 <dbl>, p100 <dbl>
[39m
# Select all columns except those from year to day (exclude)
describe(carseats, -(Sales:Income))
[38;5;246m# A tibble: 5 × 26
[39m
described_variables n na mean sd se_mean IQR skewness kurtosis
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Advertising 400 0 6.64 6.65 0.333 12 0.640 -
[31m0
[39m
[31m.
[39m
[31m545
[39m
[38;5;250m2
[39m Population 400 0 265. 147. 7.37 260. -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m51
[4m2
[24m
[39m -
[31m1
[39m
[31m.
[39m
[31m20
[39m
[38;5;250m3
[39m Price 400 0 116. 23.7 1.18 31 -
[31m0
[39m
[31m.
[39m
[31m125
[39m 0.452
[38;5;250m4
[39m Age 400 0 53.3 16.2 0.810 26.2 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m77
[4m2
[24m
[39m -
[31m1
[39m
[31m.
[39m
[31m13
[39m
[38;5;246m# ℹ 1 more row
[39m
[38;5;246m# ℹ 17 more variables: p00 <dbl>, p01 <dbl>, p05 <dbl>, p10 <dbl>, p20 <dbl>,
[39m
[38;5;246m# p25 <dbl>, p30 <dbl>, p40 <dbl>, p50 <dbl>, p60 <dbl>, p70 <dbl>,
[39m
[38;5;246m# p75 <dbl>, p80 <dbl>, p90 <dbl>, p95 <dbl>, p99 <dbl>, p100 <dbl>
[39mThe describe() function can be sorted by
left or right skewed size(skewness) using
dplyr.:
carseats %>%
describe() %>%
select(described_variables, skewness, mean, p25, p50, p75) %>%
filter(!is.na(skewness)) %>%
arrange(desc(abs(skewness)))
[38;5;246m# A tibble: 8 × 6
[39m
described_variables skewness mean p25 p50 p75
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Advertising 0.640 6.64 0 5 12
[38;5;250m2
[39m Sales 0.186 7.50 5.39 7.49 9.32
[38;5;250m3
[39m Price -
[31m0
[39m
[31m.
[39m
[31m125
[39m 116. 100 117 131
[38;5;250m4
[39m Age -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m77
[4m2
[24m
[39m 53.3 39.8 54.5 66
[38;5;246m# ℹ 4 more rows
[39mThe describe() function supports the
group_by() function syntax of the dplyr
package.
carseats %>%
group_by(US) %>%
describe(Sales, Income)
[38;5;246m# A tibble: 4 × 27
[39m
described_variables US n na mean sd se_mean IQR skewness
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Income No 130 12 65.8 28.2 2.48 50 0.100
[4m0
[24m
[38;5;250m2
[39m Income Yes 250 8 70.4 27.9 1.77 48 0.019
[4m9
[24m
[38;5;250m3
[39m Sales No 142 0 6.82 2.60 0.218 3.44 0.323
[38;5;250m4
[39m Sales Yes 258 0 7.87 2.88 0.179 4.23 0.076
[4m0
[24m
[38;5;246m# ℹ 18 more variables: kurtosis <dbl>, p00 <dbl>, p01 <dbl>, p05 <dbl>,
[39m
[38;5;246m# p10 <dbl>, p20 <dbl>, p25 <dbl>, p30 <dbl>, p40 <dbl>, p50 <dbl>,
[39m
[38;5;246m# p60 <dbl>, p70 <dbl>, p75 <dbl>, p80 <dbl>, p90 <dbl>, p95 <dbl>,
[39m
[38;5;246m# p99 <dbl>, p100 <dbl>
[39mcarseats %>%
group_by(US, Urban) %>%
describe(Sales, Income)
[38;5;246m# A tibble: 12 × 28
[39m
described_variables US Urban n na mean sd se_mean IQR skewness
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Income No No 42 4 60.2 29.1 4.49 45.2 0.408
[38;5;250m2
[39m Income No Yes 84 8 69.5 27.4 2.99 47 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m49
[4m7
[24m
[39m
[38;5;250m3
[39m Income No
[31mNA
[39m 4 0 48.2 24.7 12.3 40.8 -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m49
[4m6
[24m
[39m
[38;5;250m4
[39m Income Yes No 65 4 70.5 29.9 3.70 48 0.073
[4m6
[24m
[38;5;246m# ℹ 8 more rows
[39m
[38;5;246m# ℹ 18 more variables: kurtosis <dbl>, p00 <dbl>, p01 <dbl>, p05 <dbl>,
[39m
[38;5;246m# p10 <dbl>, p20 <dbl>, p25 <dbl>, p30 <dbl>, p40 <dbl>, p50 <dbl>,
[39m
[38;5;246m# p60 <dbl>, p70 <dbl>, p75 <dbl>, p80 <dbl>, p90 <dbl>, p95 <dbl>,
[39m
[38;5;246m# p99 <dbl>, p100 <dbl>
[39mTest of normality on numeric variables using
normality()
normality() performs a normality test on numerical data.
Shapiro-Wilk normality test is performed. When the number
of observations exceeds 5000, it is tested after extracting 5000 samples
by random simple sampling.
The variables of the tbl_df object returned by
normality() are as follows.
-
statistic: Statistics of the Shapiro-Wilk test -
p_value: p-value of the Shapiro-Wilk test -
sample: Number of sample observations performed Shapiro-Wilk test
normality() performs the normality test for all
numerical variables of carseats as follows.:
normality(carseats)
[38;5;246m# A tibble: 8 × 4
[39m
vars statistic p_value sample
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Sales 0.995 2.54
[38;5;246me
[39m
[31m- 1
[39m 400
[38;5;250m2
[39m CompPrice 0.998 9.77
[38;5;246me
[39m
[31m- 1
[39m 400
[38;5;250m3
[39m Income 0.961 1.52
[38;5;246me
[39m
[31m- 8
[39m 400
[38;5;250m4
[39m Advertising 0.874 1.49
[38;5;246me
[39m
[31m-17
[39m 400
[38;5;246m# ℹ 4 more rows
[39mThe following example performs a normality test on only a few selected variables.
# Select columns by name
normality(carseats, Sales, CompPrice, Income)
[38;5;246m# A tibble: 3 × 4
[39m
vars statistic p_value sample
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Sales 0.995 0.254 400
[38;5;250m2
[39m CompPrice 0.998 0.977 400
[38;5;250m3
[39m Income 0.961 0.000
[4m0
[24m
[4m0
[24m
[4m0
[24m015
[4m2
[24m 400
# Select all columns between year and day (inclusive)
normality(carseats, Sales:Income)
[38;5;246m# A tibble: 3 × 4
[39m
vars statistic p_value sample
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Sales 0.995 0.254 400
[38;5;250m2
[39m CompPrice 0.998 0.977 400
[38;5;250m3
[39m Income 0.961 0.000
[4m0
[24m
[4m0
[24m
[4m0
[24m015
[4m2
[24m 400
# Select all columns except those from year to day (inclusive)
normality(carseats, -(Sales:Income))
[38;5;246m# A tibble: 5 × 4
[39m
vars statistic p_value sample
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Advertising 0.874 1.49
[38;5;246me
[39m
[31m-17
[39m 400
[38;5;250m2
[39m Population 0.952 4.08
[38;5;246me
[39m
[31m-10
[39m 400
[38;5;250m3
[39m Price 0.996 3.90
[38;5;246me
[39m
[31m- 1
[39m 400
[38;5;250m4
[39m Age 0.957 1.86
[38;5;246me
[39m
[31m- 9
[39m 400
[38;5;246m# ℹ 1 more row
[39mYou can use dplyr to sort variables that do not follow a
normal distribution in order of p_value:
library(dplyr)
carseats %>%
normality() %>%
filter(p_value <= 0.01) %>%
arrange(abs(p_value))
[38;5;246m# A tibble: 5 × 4
[39m
vars statistic p_value sample
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Advertising 0.874 1.49
[38;5;246me
[39m
[31m-17
[39m 400
[38;5;250m2
[39m Education 0.924 2.43
[38;5;246me
[39m
[31m-13
[39m 400
[38;5;250m3
[39m Population 0.952 4.08
[38;5;246me
[39m
[31m-10
[39m 400
[38;5;250m4
[39m Age 0.957 1.86
[38;5;246me
[39m
[31m- 9
[39m 400
[38;5;246m# ℹ 1 more row
[39mIn particular, the Advertising variable is considered to
be the most out of the normal distribution
The normality() function supports the
group_by() function syntax in the dplyr
package.
carseats %>%
group_by(ShelveLoc, US) %>%
normality(Income) %>%
arrange(desc(p_value))
[38;5;246m# A tibble: 6 × 6
[39m
variable ShelveLoc US statistic p_value sample
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Income Bad No 0.969 0.470 34
[38;5;250m2
[39m Income Bad Yes 0.958 0.034
[4m3
[24m 62
[38;5;250m3
[39m Income Good No 0.902 0.032
[4m8
[24m 24
[38;5;250m4
[39m Income Good Yes 0.955 0.029
[4m6
[24m 61
[38;5;246m# ℹ 2 more rows
[39mThe Income variable does not follow the normal
distribution. However, where US is No and
ShelveLoc is Good and Bad at the
significance level 0.01, it follows the normal distribution.
The following example performs the
normality test of log(Income) for each combination of
ShelveLoc and US categorical variables to
search for variables that follow the normal distribution.
carseats %>%
mutate(log_income = log(Income)) %>%
group_by(ShelveLoc, US) %>%
normality(log_income) %>%
filter(p_value > 0.01)
[38;5;246m# A tibble: 1 × 6
[39m
variable ShelveLoc US statistic p_value sample
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m log_income Bad No 0.940 0.073
[4m7
[24m 34Visualization of normality of numerical variables using
plot_normality()
plot_normality() visualizes the normality of numeric
data.
The information visualized by plot_normality() is as
follows.:
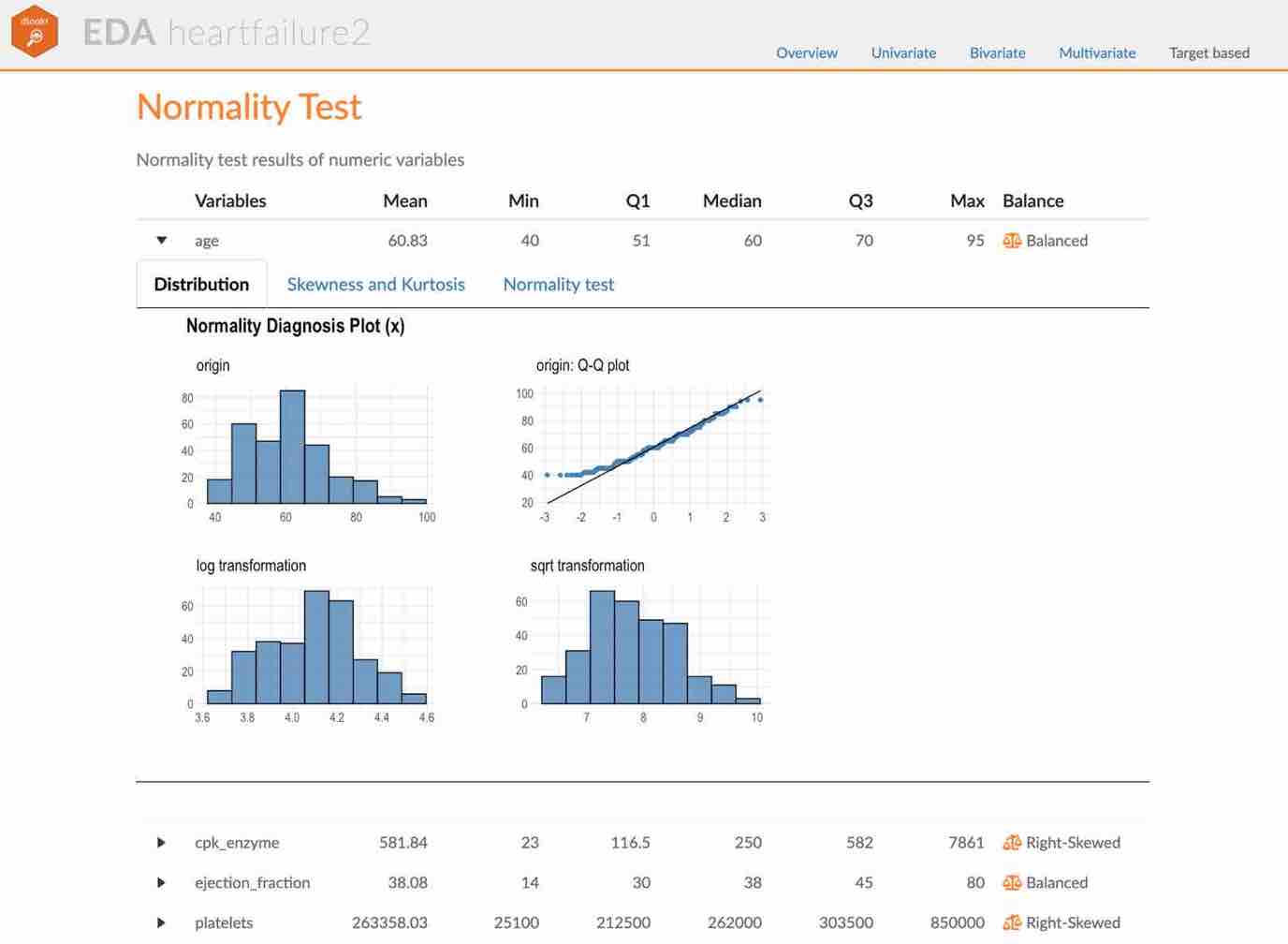
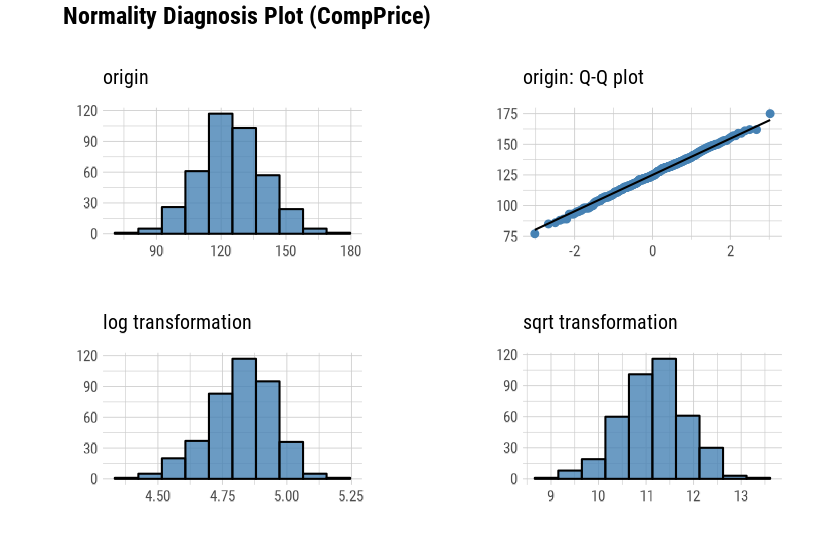
Histogram of original dataQ-Q plot of original datahistogram of log transformed dataHistogram of square root transformed data
The data analysis often encounters numerical data that follows the
power-law distribution. Since the numerical data that
follows the power-law distribution is converted into a
normal distribution by performing the log or
sqrt transformation, so draw a histogram of the
log and sqrt transformed data.
plot_normality() can also specify several variables like
normality() function.
# Select columns by name
plot_normality(carseats, Sales, CompPrice)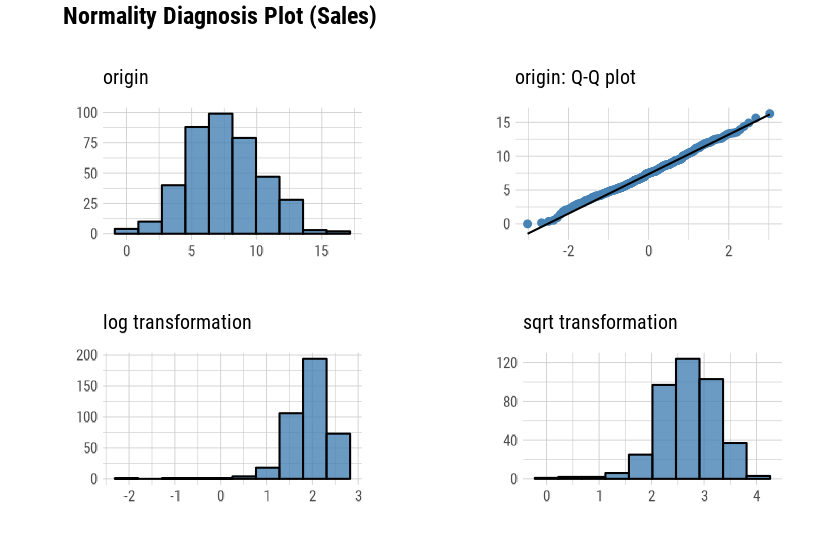
The plot_normality() function also supports the
group_by() function syntax in the dplyr
package.
EDA of bivariate data
Calculation of correlation coefficient using
correlate()
correlate() calculates the correlation coefficient of
all combinations of carseats numerical variables as
follows:
correlate(carseats)
[38;5;246m# A tibble: 56 × 3
[39m
var1 var2 coef_corr
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m CompPrice Sales 0.064
[4m1
[24m
[38;5;250m2
[39m Income Sales 0.151
[38;5;250m3
[39m Advertising Sales 0.270
[38;5;250m4
[39m Population Sales 0.050
[4m5
[24m
[38;5;246m# ℹ 52 more rows
[39mThe following example performs a normality test only on combinations that include several selected variables.
# Select columns by name
correlate(carseats, Sales, CompPrice, Income)
[38;5;246m# A tibble: 21 × 3
[39m
var1 var2 coef_corr
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m CompPrice Sales 0.064
[4m1
[24m
[38;5;250m2
[39m Income Sales 0.151
[38;5;250m3
[39m Sales CompPrice 0.064
[4m1
[24m
[38;5;250m4
[39m Income CompPrice -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m76
[4m1
[24m
[39m
[38;5;246m# ℹ 17 more rows
[39m
# Select all columns between year and day (include)
correlate(carseats, Sales:Income)
[38;5;246m# A tibble: 21 × 3
[39m
var1 var2 coef_corr
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m CompPrice Sales 0.064
[4m1
[24m
[38;5;250m2
[39m Income Sales 0.151
[38;5;250m3
[39m Sales CompPrice 0.064
[4m1
[24m
[38;5;250m4
[39m Income CompPrice -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m76
[4m1
[24m
[39m
[38;5;246m# ℹ 17 more rows
[39m
# Select all columns except those from year to day (exclude)
correlate(carseats, -(Sales:Income))
[38;5;246m# A tibble: 35 × 3
[39m
var1 var2 coef_corr
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Advertising Sales 0.270
[38;5;250m2
[39m Population Sales 0.050
[4m5
[24m
[38;5;250m3
[39m Price Sales -
[31m0
[39m
[31m.
[39m
[31m445
[39m
[38;5;250m4
[39m Age Sales -
[31m0
[39m
[31m.
[39m
[31m232
[39m
[38;5;246m# ℹ 31 more rows
[39mcorrelate() produces
two pairs of variables. So the following example uses
filter() to get the correlation coefficient for
a pair of variable combinations:
carseats %>%
correlate(Sales:Income) %>%
filter(as.integer(var1) > as.integer(var2))
[38;5;246m# A tibble: 3 × 3
[39m
var1 var2 coef_corr
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m CompPrice Sales 0.064
[4m1
[24m
[38;5;250m2
[39m Income Sales 0.151
[38;5;250m3
[39m Income CompPrice -
[31m0
[39m
[31m.
[39m
[31m0
[39m
[31m76
[4m1
[24m
[39mThe correlate() also supports the
group_by() function syntax in the dplyr
package.
tab_corr <- carseats %>%
filter(ShelveLoc == "Good") %>%
group_by(Urban, US) %>%
correlate(Sales) %>%
filter(abs(coef_corr) > 0.5)
tab_corr
[38;5;246m# A tibble: 10 × 5
[39m
Urban US var1 var2 coef_corr
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m No No Sales Population -
[31m0
[39m
[31m.
[39m
[31m530
[39m
[38;5;250m2
[39m No No Sales Price -
[31m0
[39m
[31m.
[39m
[31m838
[39m
[38;5;250m3
[39m No Yes Sales Price -
[31m0
[39m
[31m.
[39m
[31m630
[39m
[38;5;250m4
[39m Yes No Sales Price -
[31m0
[39m
[31m.
[39m
[31m833
[39m
[38;5;246m# ℹ 6 more rows
[39mVisualization of the correlation matrix using
plot.correlate()
plot.correlate() visualizes the correlation matrix with
correlate class.
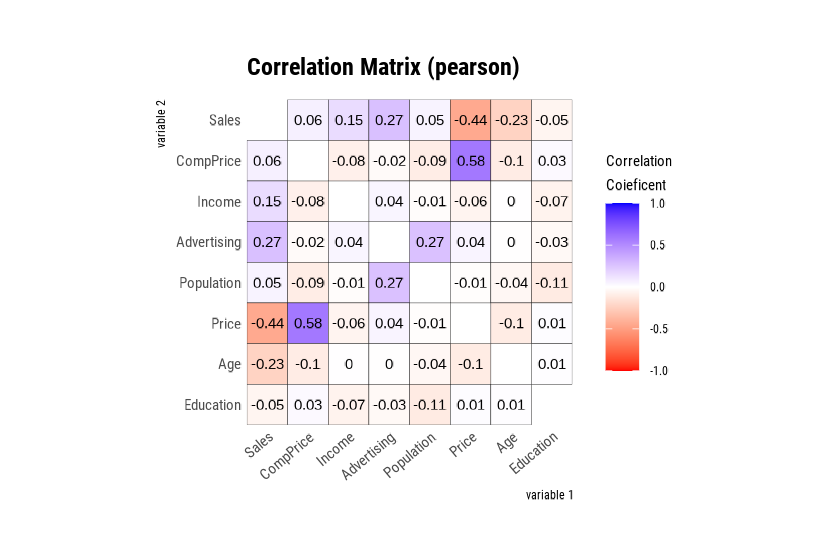
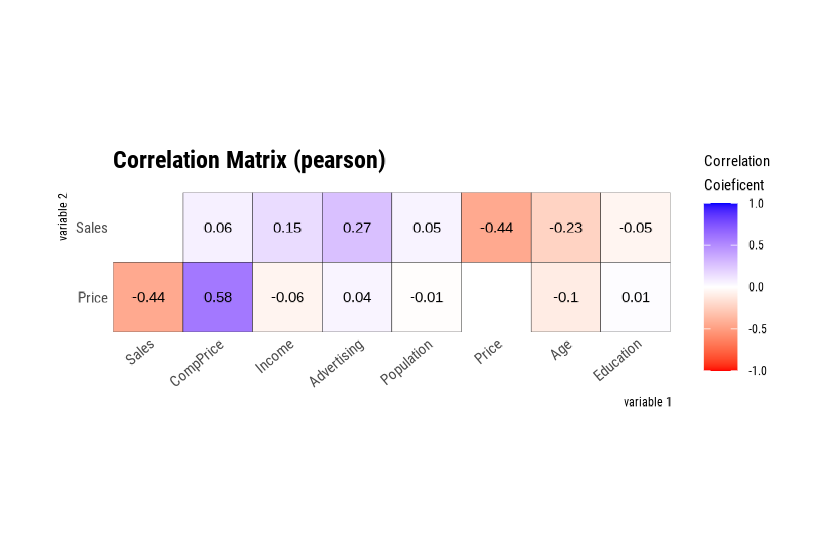
plot.correlate() can also specify multiple variables,
like the correlate() function. The following visualize the
correlation matrix, including several selected variables.
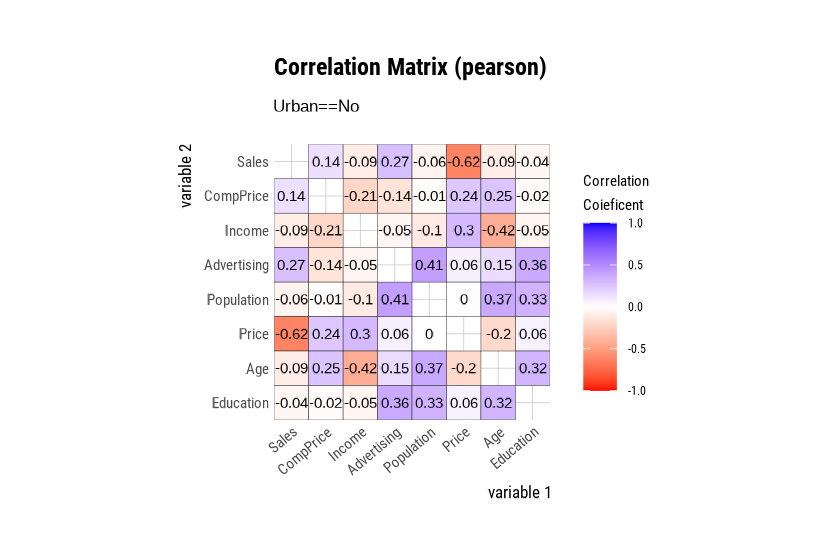
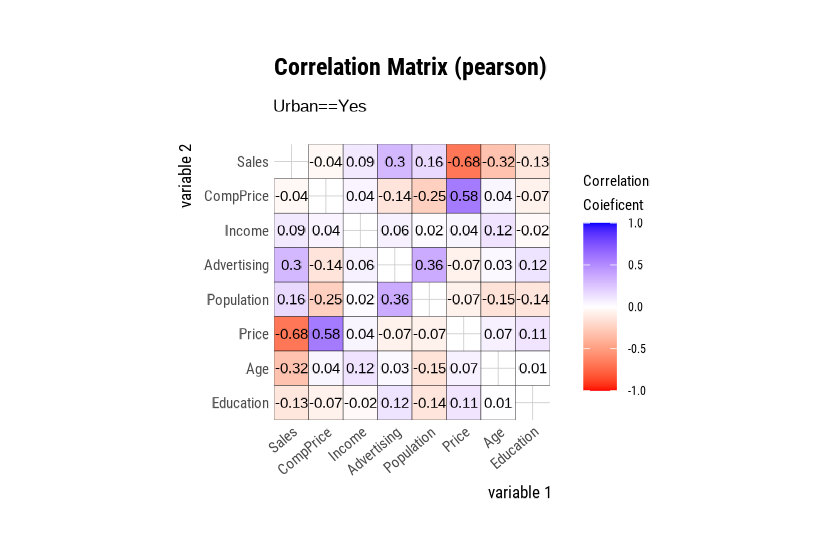
The plot.correlate() function also supports the
group_by() function syntax in the dplyr
package.
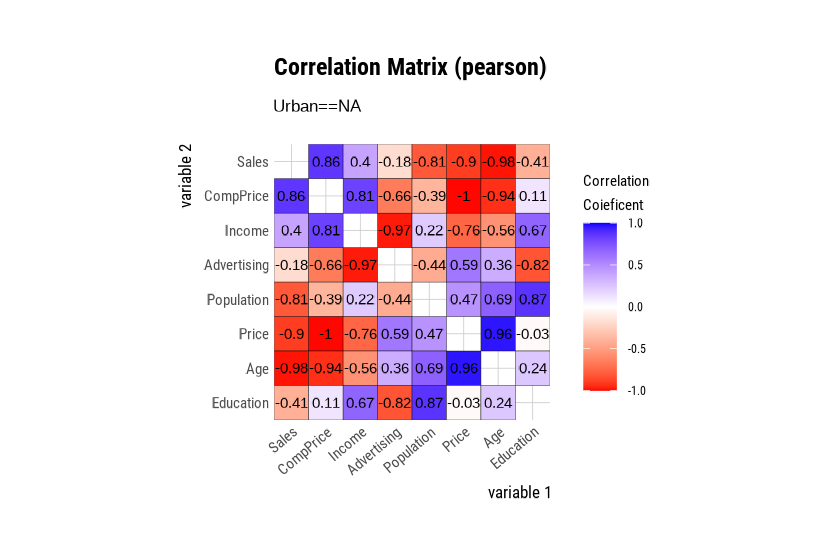
EDA based on target variable
Definition of target variable
To perform EDA based on the target variable, you must
create a target_by class object. target_by()
creates a target_by class with an object inheriting
data.frame or data.frame. target_by() is similar to
group_by() in dplyr which creates
grouped_df. The difference is that you specify only one
variable.
The following is an example of specifying US as the
target variable in carseats data.frame.:
categ <- target_by(carseats, US)EDA when target variable is categorical variable
Let’s perform EDA when the target variable is categorical. When the
categorical variable US is the target variable, we examine
the relationship between the target variable and the predictor.
Cases where predictors are numeric variable
relate() shows the relationship between the target
variable and the predictor. The following example shows the relationship
between Sales and the target variable US. The
predictor Sales is a numeric variable. In this case, the
descriptive statistics are shown for each level of the target
variable.
# If the variable of interest is a numerical variable
cat_num <- relate(categ, Sales)
cat_num
[38;5;246m# A tibble: 3 × 27
[39m
described_variables US n na mean sd se_mean IQR skewness
[3m
[38;5;246m<chr>
[39m
[23m
[3m
[38;5;246m<fct>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<int>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[3m
[38;5;246m<dbl>
[39m
[23m
[38;5;250m1
[39m Sales No 142 0 6.82 2.60 0.218 3.44 0.323
[38;5;250m2
[39m Sales Yes 258 0 7.87 2.88 0.179 4.23 0.076
[4m0
[24m
[38;5;250m3
[39m Sales total 400 0 7.50 2.82 0.141 3.93 0.186
[38;5;246m# ℹ 18 more variables: kurtosis <dbl>, p00 <dbl>, p01 <dbl>, p05 <dbl>,
[39m
[38;5;246m# p10 <dbl>, p20 <dbl>, p25 <dbl>, p30 <dbl>, p40 <dbl>, p50 <dbl>,
[39m
[38;5;246m# p60 <dbl>, p70 <dbl>, p75 <dbl>, p80 <dbl>, p90 <dbl>, p95 <dbl>,
[39m
[38;5;246m# p99 <dbl>, p100 <dbl>
[39m
summary(cat_num)
described_variables US n na mean
Length:3 No :1 Min. :142.0 Min. :0 Min. :6.823
Class :character Yes :1 1st Qu.:200.0 1st Qu.:0 1st Qu.:7.160
Mode :character total:1 Median :258.0 Median :0 Median :7.496
Mean :266.7 Mean :0 Mean :7.395
3rd Qu.:329.0 3rd Qu.:0 3rd Qu.:7.682
Max. :400.0 Max. :0 Max. :7.867
sd se_mean IQR skewness
Min. :2.603 Min. :0.1412 Min. :3.442 Min. :0.07603
1st Qu.:2.713 1st Qu.:0.1602 1st Qu.:3.686 1st Qu.:0.13080
Median :2.824 Median :0.1791 Median :3.930 Median :0.18556
Mean :2.768 Mean :0.1796 Mean :3.866 Mean :0.19489
3rd Qu.:2.851 3rd Qu.:0.1988 3rd Qu.:4.077 3rd Qu.:0.25432
Max. :2.877 Max. :0.2184 Max. :4.225 Max. :0.32308
kurtosis p00 p01 p05
Min. :-0.32638 Min. :0.0000 Min. :0.4675 Min. :3.147
1st Qu.:-0.20363 1st Qu.:0.0000 1st Qu.:0.6868 1st Qu.:3.148
Median :-0.08088 Median :0.0000 Median :0.9062 Median :3.149
Mean : 0.13350 Mean :0.1233 Mean :1.0072 Mean :3.183
3rd Qu.: 0.36344 3rd Qu.:0.1850 3rd Qu.:1.2771 3rd Qu.:3.200
Max. : 0.80776 Max. :0.3700 Max. :1.6480 Max. :3.252
p10 p20 p25 p30
Min. :3.917 Min. :4.754 Min. :5.080 Min. :5.306
1st Qu.:4.018 1st Qu.:4.910 1st Qu.:5.235 1st Qu.:5.587
Median :4.119 Median :5.066 Median :5.390 Median :5.867
Mean :4.073 Mean :5.051 Mean :5.411 Mean :5.775
3rd Qu.:4.152 3rd Qu.:5.199 3rd Qu.:5.576 3rd Qu.:6.010
Max. :4.184 Max. :5.332 Max. :5.763 Max. :6.153
p40 p50 p60 p70
Min. :5.994 Min. :6.660 Min. :7.496 Min. :7.957
1st Qu.:6.301 1st Qu.:7.075 1st Qu.:7.787 1st Qu.:8.386
Median :6.608 Median :7.490 Median :8.078 Median :8.815
Mean :6.506 Mean :7.313 Mean :8.076 Mean :8.740
3rd Qu.:6.762 3rd Qu.:7.640 3rd Qu.:8.366 3rd Qu.:9.132
Max. :6.916 Max. :7.790 Max. :8.654 Max. :9.449
p75 p80 p90 p95
Min. :8.523 Min. : 8.772 Min. : 9.349 Min. :11.28
1st Qu.:8.921 1st Qu.: 9.265 1st Qu.:10.325 1st Qu.:11.86
Median :9.320 Median : 9.758 Median :11.300 Median :12.44
Mean :9.277 Mean : 9.665 Mean :10.795 Mean :12.08
3rd Qu.:9.654 3rd Qu.:10.111 3rd Qu.:11.518 3rd Qu.:12.49
Max. :9.988 Max. :10.464 Max. :11.736 Max. :12.54
p99 p100
Min. :13.64 Min. :14.90
1st Qu.:13.78 1st Qu.:15.59
Median :13.91 Median :16.27
Mean :13.86 Mean :15.81
3rd Qu.:13.97 3rd Qu.:16.27
Max. :14.03 Max. :16.27 plot() visualizes the relate class object
created by relate() as the relationship between the target
and predictor variables. The relationship between US and
Sales is visualized by a density plot.
plot(cat_num)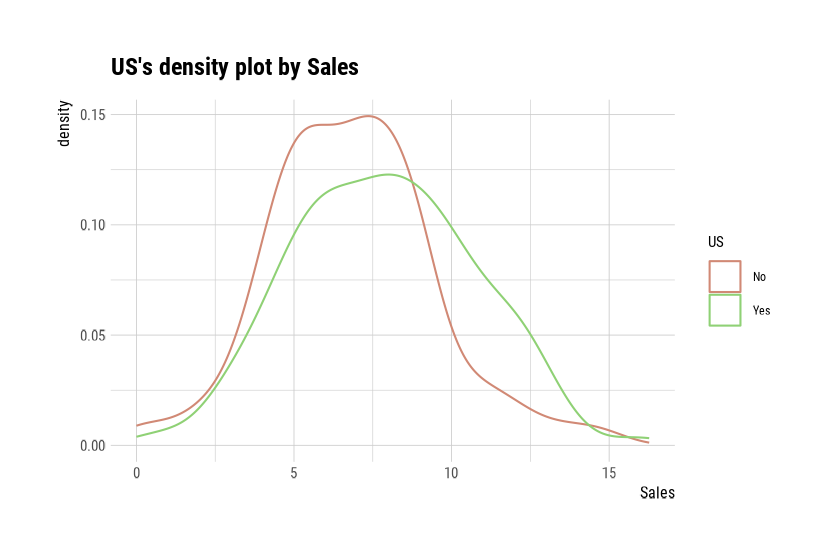
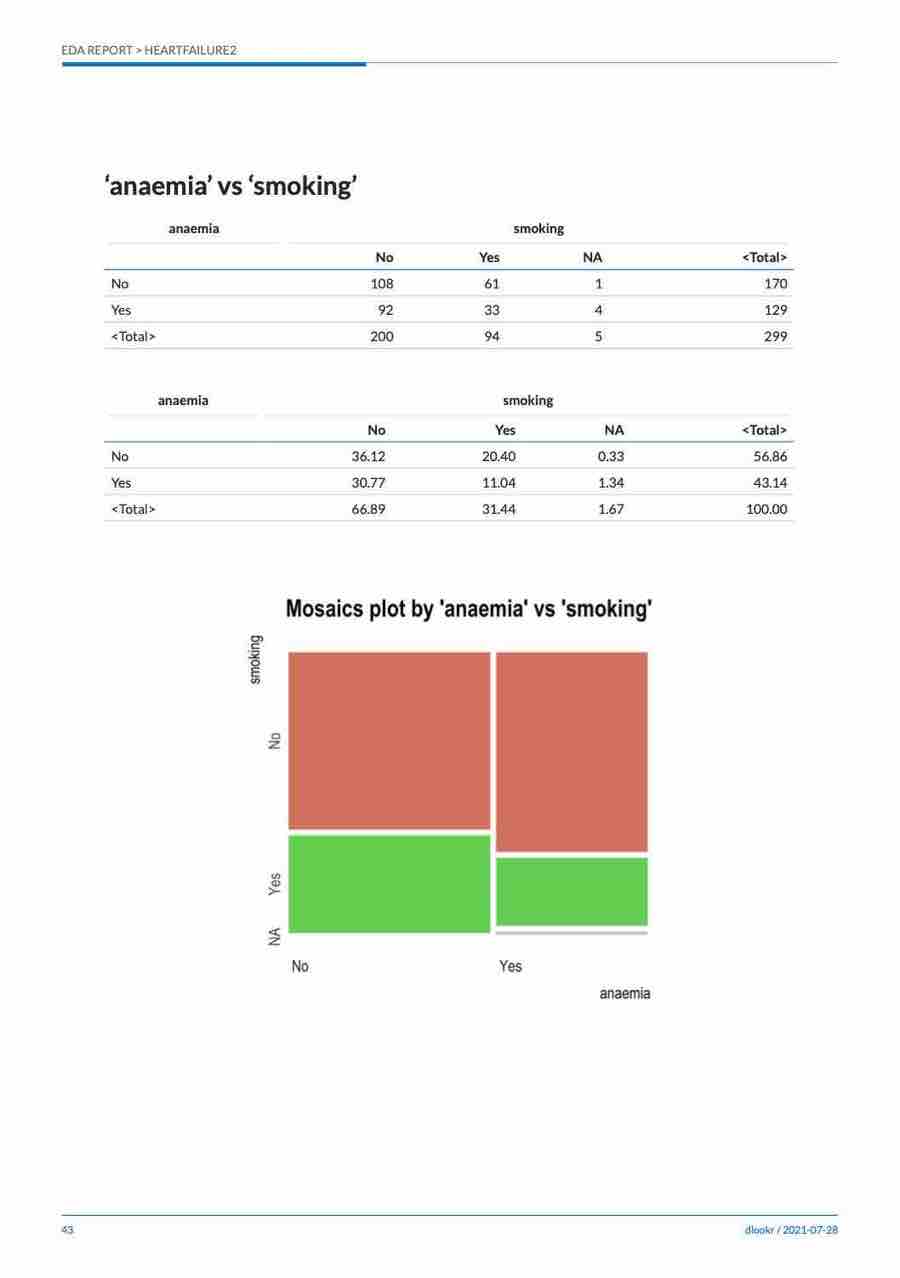
Cases where predictors are categorical variable
The following example shows the relationship between
ShelveLoc and the target variable US. The
predictor variable ShelveLoc is categorical. This case
illustrates the contingency table of two variables. The
summary() function performs an
independence test on the contingency table.
# If the variable of interest is a categorical variable
cat_cat <- relate(categ, ShelveLoc)
cat_cat
ShelveLoc
US Bad Good Medium
No 34 24 84
Yes 62 61 135
summary(cat_cat)
Call: xtabs(formula = formula_str, data = data, addNA = TRUE)
Number of cases in table: 400
Number of factors: 2
Test for independence of all factors:
Chisq = 2.7397, df = 2, p-value = 0.2541plot() visualizes the relationship between the target
variable and the predictor. A mosaics plot represents the
relationship between US and ShelveLoc.
plot(cat_cat)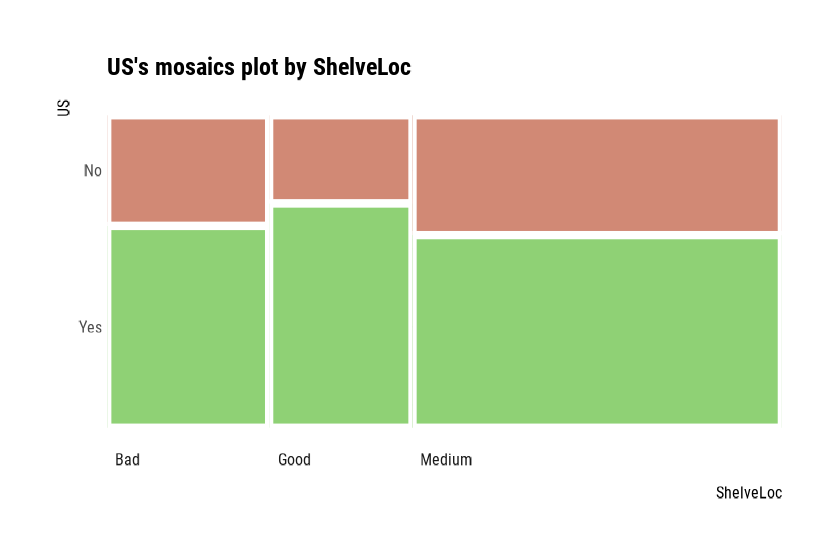
EDA when target variable is numerical variable
Let’s perform EDA when the target variable is numeric. When the
numeric variable Sales is the target variable, we examine
the relationship between the target variable and the predictor.
# If the variable of interest is a numerical variable
num <- target_by(carseats, Sales)Cases where predictors are numeric variable
The following example shows the relationship between
Price and the target variable Sales. The
predictor variable Price is numeric. In this case, it shows
the result of a simple linear model of the
target ~ predictor formula. The summary()
function expresses the details of the model.
# If the variable of interest is a numerical variable
num_num <- relate(num, Price)
num_num
Call:
lm(formula = formula_str, data = data)
Coefficients:
(Intercept) Price
13.64192 -0.05307
summary(num_num)
Call:
lm(formula = formula_str, data = data)
Residuals:
Min 1Q Median 3Q Max
-6.5224 -1.8442 -0.1459 1.6503 7.5108
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 13.641915 0.632812 21.558 <2e-16 ***
Price -0.053073 0.005354 -9.912 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.532 on 398 degrees of freedom
Multiple R-squared: 0.198, Adjusted R-squared: 0.196
F-statistic: 98.25 on 1 and 398 DF, p-value: < 2.2e-16plot() visualizes the relationship between the target
and predictor variables. The relationship between Sales and
Price is pictured with a scatter plot. The figure on the
left shows the scatter plot of Sales and Price
and the confidence interval of the regression line and regression line.
The figure on the right shows the relationship between the original data
and the predicted values of the linear model as a scatter plot. If there
is a linear relationship between the two variables, the scatter plot of
the observations converges on the red diagonal line.
plot(num_num)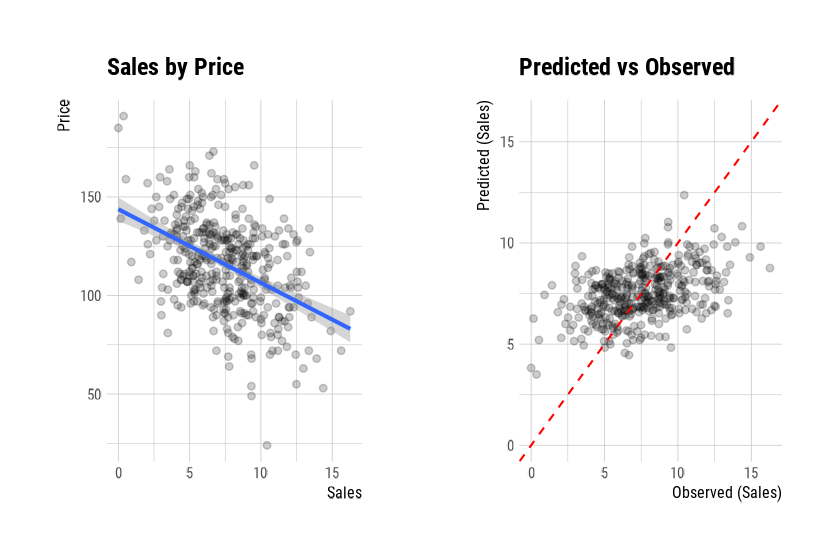
The scatter plot of the data with many observations is output as
overlapping points. This makes it difficult to judge the relationship
between the two variables. It also takes a long time to perform the
visualization. In this case, the above problem can be solved by
hexabin plot.
In plot(), the hex_thres argument provides
a basis for drawing hexabin plot. If the number of
observations is greater than hex_thres, draw a
hexabin plot.
The following example visualizes the hexabin plot rather
than the scatter plot by specifying 350 for the hex_thres
argument. This is because the number of observations is 400.
plot(num_num, hex_thres = 350)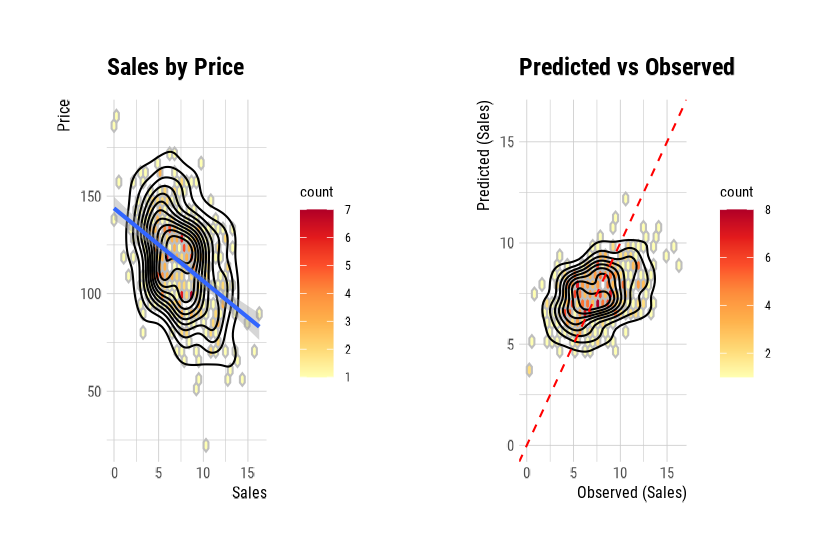
Cases where predictors are categorical variable
The following example shows the relationship between
ShelveLoc and the target variable Sales. The
predictor ShelveLoc is a categorical variable and displays
the result of a one-way ANOVA of the
target ~ predictor relationship. The results are expressed
in terms of ANOVA. The summary() function shows the
regression coefficients for each level of the predictor. In
other words, it shows detailed information about the
simple regression analysis of the
target ~ predictor relationship.
# If the variable of interest is a categorical variable
num_cat <- relate(num, ShelveLoc)
num_cat
Analysis of Variance Table
Response: Sales
Df Sum Sq Mean Sq F value Pr(>F)
ShelveLoc 2 1009.5 504.77 92.23 < 2.2e-16 ***
Residuals 397 2172.7 5.47
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(num_cat)
Call:
lm(formula = formula(formula_str), data = data)
Residuals:
Min 1Q Median 3Q Max
-7.3066 -1.6282 -0.0416 1.5666 6.1471
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.5229 0.2388 23.131 < 2e-16 ***
ShelveLocGood 4.6911 0.3484 13.464 < 2e-16 ***
ShelveLocMedium 1.7837 0.2864 6.229 1.2e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.339 on 397 degrees of freedom
Multiple R-squared: 0.3172, Adjusted R-squared: 0.3138
F-statistic: 92.23 on 2 and 397 DF, p-value: < 2.2e-16plot() visualizes the relationship between the target
variable and the predictor. A box plot represents the
relationship between Sales and ShelveLoc.
plot(num_cat)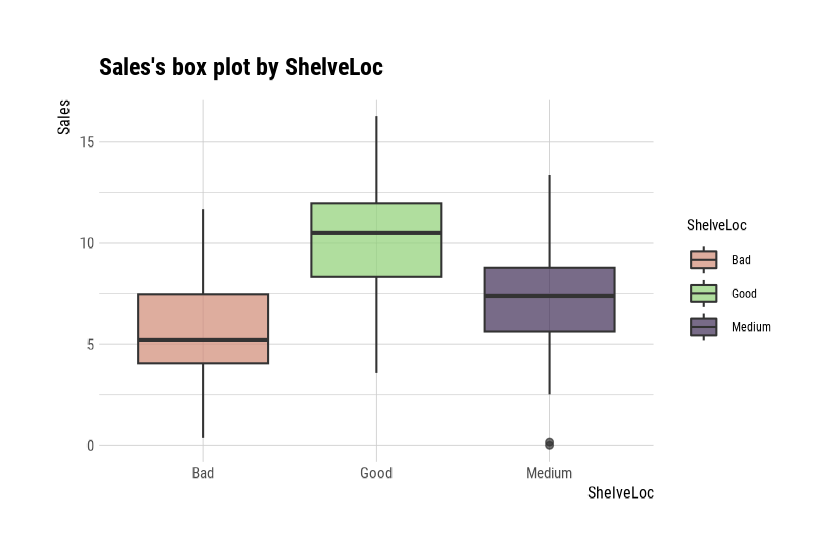
Automated report
dlookr provides two automated EDA reports:
- Web page-based dynamic reports can perform in-depth analysis through visualization and statistical tables.
- Static reports generated as PDF files or HTML files can be archived as the output of data analysis.
Create a dynamic report using eda_web_report()
eda_web_report() creates a dynamic report for objects
inherited from data.frame(tbl_df, tbl, etc) or
data.frame.
Contents of dynamic web report
The contents of the report are as follows.:
- Overview
- Data Structures
- Data Types
- Job Information
- Univariate Analysis
- Descriptive Statistics
- Normality Test
- Bivariate Analysis
- Compare Numerical Variables
- Compare Categorical Variables
- Multivariate Analysis
- Correlation Analysis
- Correlation Matrix
- Correlation Plot
- Correlation Analysis
- Target based Analysis
- Grouped Numerical Variables
- Grouped Categorical Variables
- Grouped Correlation
Some arguments for dynamic web report
eda_web_report() generates various reports with the following arguments.
- target
- target variable
- output_file
- name of the generated file.
- output_dir
- name of the directory to generate report file.
- title
- title of the report.
- subtitle
- subtitle of the report.
- author
- author of the report.
- title_color
- color of title.
- logo_img
- name of the logo image file on the top left.
- create_date
- The date on which the report is generated.
- theme
- name of theme for report. Support “orange” and “blue”.
- sample_percent
- Sample percent of data for performing EDA.
The following script creates an EDA report for the
data.frame class object, heartfailure.
heartfailure %>%
eda_web_report(target = "death_event", subtitle = "heartfailure",
output_dir = "./", output_file = "EDA.html", theme = "blue")Create a EDA report using eda_paged_report()
eda_paged_report() creates a static report for an object
inherited from data.frame(tbl_df, tbl, etc) or
data.frame.
Contents of static paged report
The contents of the report are as follows.:
- Overview
- Data Structures
- Job Information
- Univariate Analysis
- Descriptive Statistics
- Numerical Variables
- Categorical Variables
- Normality Test
- Descriptive Statistics
- Bivariate Analysis
- Compare Numerical Variables
- Compare Categorical Variables
- Multivariate Analysis
- Correlation Analysis
- Correlation Coefficient Matrix
- Correlation Plot
- Correlation Analysis
- Target based Analysis
- Grouped Numerical Variables
- Grouped Categorical Variables
- Grouped Correlation
Some arguments for static paged report
eda_paged_report() generates various reports with the following arguments.
- target
- target variable
- output_format
- report output type. Choose either “pdf” or “html”.
- output_file
- name of the generated file.
- output_dir
- name of the directory to generate the report file.
- title
- title of the report.
- subtitle
- subtitle of the report.
- abstract_title
- abstract of the report
- author
- author of the report.
- title_color
- color of title.
- subtitle_color
- color of subtitle.
- logo_img
- the name of the logo image file is on the top left.
- cover_img
- name of cover image file on center.
- create_date
- The date on which the report is generated.
- theme
- name of the theme for the report. Support “orange” and “blue”.
- sample_percent
- Sample percent of data for performing EDA.
The following script creates an EDA report for the
data.frame class object, heartfailure.
heartfailure %>%
eda_paged_report(target = "death_event", subtitle = "heartfailure",
output_dir = "./", output_file = "EDA.pdf", theme = "blue")Exploratory data analysis for tables in DBMS
EDA function for a table of DBMS supports In-database mode that performs SQL operations on the DBMS side. If the data size is large, using In-database mode is faster.
It is challenging to obtain anomalies or to implement the sampling-based algorithm in SQL of DBMS. So, some functions do not yet support In-database mode. In this case, it is performed in In-memory mode, where table data is brought to the R side and calculated. In this case, if the data size is large, the execution speed may be slow. It supports the collect_size argument, allowing you to import the specified number of data samples into R.
- In-database support functions
- none
- In-database not support functions
Preparing table data
Copy the carseats data frame to the SQLite DBMS and
create it as a table named TB_CARSEATS. Mysql/MariaDB,
PostgreSQL, Oracle DBMS, and other DBMS are also available for your
environment.
library(dplyr)
carseats <- Carseats
carseats[sample(seq(NROW(carseats)), 20), "Income"] <- NA
carseats[sample(seq(NROW(carseats)), 5), "Urban"] <- NA
# connect DBMS
con_sqlite <- DBI::dbConnect(RSQLite::SQLite(), ":memory:")
# copy carseats to the DBMS with a table named TB_CARSEATS
copy_to(con_sqlite, carseats, name = "TB_CARSEATS", overwrite = TRUE)Calculating descriptive statistics of numerical column of table in the DBMS
Use dplyr::tbl() to create a tbl_dbi object, then use it
as a data frame object. The data argument of all EDA functions is
specified as a tbl_dbi object instead of a data frame object.
# Positive values select variables
con_sqlite %>%
tbl("TB_CARSEATS") %>%
describe(Sales, CompPrice, Income)
# Negative values to drop variables, and In-memory mode and collect size is 200
con_sqlite %>%
tbl("TB_CARSEATS") %>%
describe(-Sales, -CompPrice, -Income, collect_size = 200)
# Find the statistic of all numerical variables by 'ShelveLoc' and 'US',
# and extract only those with the 'ShelveLoc' variable level as "Good".
con_sqlite %>%
tbl("TB_CARSEATS") %>%
group_by(ShelveLoc, US) %>%
describe() %>%
filter(ShelveLoc == "Good")
# extract only those with 'Urban' variable level is "Yes",
# and find 'Sales' statistics by 'ShelveLoc' and 'US'
con_sqlite %>%
tbl("TB_CARSEATS") %>%
filter(Urban == "Yes") %>%
group_by(ShelveLoc, US) %>%
describe(Sales)Test of normality on numeric columns using in the DBMS
# Test all numerical variables by 'ShelveLoc' and 'US',
# and extract only those with the 'ShelveLoc' variable level is "Good".
con_sqlite %>%
tbl("TB_CARSEATS") %>%
group_by(ShelveLoc, US) %>%
normality() %>%
filter(ShelveLoc == "Good")
# extract only those with 'Urban' variable level is "Yes",
# and test 'Sales' by 'ShelveLoc' and 'US'
con_sqlite %>%
tbl("TB_CARSEATS") %>%
filter(Urban == "Yes") %>%
group_by(ShelveLoc, US) %>%
normality(Sales)
# Test log(Income) variables by 'ShelveLoc' and 'US',
# and extract only p.value greater than 0.01.
# SQLite extension functions for log transformation
RSQLite::initExtension(con_sqlite)
con_sqlite %>%
tbl("TB_CARSEATS") %>%
mutate(log_income = log(Income)) %>%
group_by(ShelveLoc, US) %>%
normality(log_income) %>%
filter(p_value > 0.01)Normalization visualization of numerical column in the DBMS
# Extract only those with the 'ShelveLoc' variable level is "Good",
# and plot 'Income' by 'US'
# The result is the same as the data.frame, but not displayed here. Reference above in document.
con_sqlite %>%
tbl("TB_CARSEATS") %>%
filter(ShelveLoc == "Good") %>%
group_by(US) %>%
plot_normality(Income)Compute the correlation coefficient between two columns of the table in DBMS
# Correlation coefficient
# that eliminates redundant combination of variables
con_sqlite %>%
tbl("TB_CARSEATS") %>%
correlate() %>%
filter(as.integer(var1) > as.integer(var2))
con_sqlite %>%
tbl("TB_CARSEATS") %>%
correlate(Sales, Price) %>%
filter(as.integer(var1) > as.integer(var2))
# Compute the correlation coefficient of the Sales variable by 'ShelveLoc'
# and 'US' variables. And extract only those with absolute
# value of the correlation coefficient is more significant than 0.5
con_sqlite %>%
tbl("TB_CARSEATS") %>%
group_by(ShelveLoc, US) %>%
correlate(Sales) %>%
filter(abs(coef_corr) >= 0.5)
# Extract only those with the 'ShelveLoc' variable level is "Good",
# and compute the correlation coefficient of the 'Sales' variable
# by 'Urban' and 'US' variables.
# And the correlation coefficient is negative and smaller than 0.5
con_sqlite %>%
tbl("TB_CARSEATS") %>%
filter(ShelveLoc == "Good") %>%
group_by(Urban, US) %>%
correlate(Sales) %>%
filter(coef_corr < 0) %>%
filter(abs(coef_corr) > 0.5)Visualize correlation plot of numerical columns in the DBMS
# Extract only those with 'ShelveLoc' variable level is "Good",
# and visualize correlation plot of 'Sales' variable by 'Urban'
# and 'US' variables.
# The result is the same as the data.frame, but not displayed here. Reference above in document.
con_sqlite %>%
tbl("TB_CARSEATS") %>%
filter(ShelveLoc == "Good") %>%
group_by(Urban) %>%
correlate() %>%
plot(Sales)EDA based on target variable
The following is an EDA where the target column is a character, and the predictor column is a numeric type.
# If the target variable is a categorical variable
categ <- target_by(con_sqlite %>% tbl("TB_CARSEATS") , US)
# If the variable of interest is a numerical variable
cat_num <- relate(categ, Sales)
cat_num
summary(cat_num)
# The result is the same as the data.frame, but not displayed here. Reference above in document.
plot(cat_num)Reporting the information of EDA for table of the DBMS
The following shows several examples of creating an EDA report for a DBMS table.
Using the collect_size argument, you can perform EDA
with the corresponding number of sample data. If the number of data is
huge, use collect_size.
# create a web report file.
con_sqlite %>%
tbl("TB_CARSEATS") %>%
eda_web_report()
# create a pdf file. the file name is EDA.pdf, and the collect size is 350
con_sqlite %>%
tbl("TB_CARSEATS") %>%
eda_paged_report(collect_size = 350, output_file = "EDA.pdf")